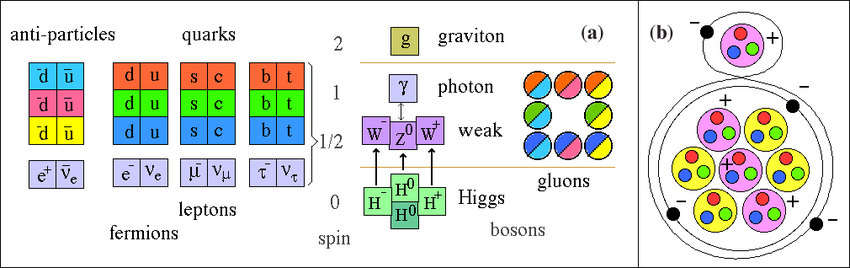
In the quantum world, every particle spins — but not in the way a ball or planet does.
This “spin” isn’t a literal rotation; it’s a built-in form of intrinsic angular momentum, a kind of twist of existence that defines what the particle truly is.
Some particles have integer spins (like 0, 1, or 2). Others have half-integer spins (like ½, 3⁄2, 5⁄2…).
And that simple difference — that tiny half — divides the universe into two great families:
Bosons and Fermions.
What Does “Half-Integer Spin” Mean?
In simplest terms:
A particle with half-integer spin is one that needs to be turned two full times (720°) to return to its original state.
It’s like twisting a ribbon — one turn flips it, but only after a second turn does it settle back into its true shape.
That’s what makes half-integer spin particles so wonderfully strange.
Electrons, protons, and neutrons — the very stuff of matter — all have spin ½.
It’s a defining fingerprint of what makes them fermions.
The Quantum Rule It Creates
Because they have half-integer spin, these particles obey something called the Pauli Exclusion Principle —
No two identical fermions can occupy the same quantum state at the same time.
That’s why electrons stack neatly into atomic shells instead of collapsing together.
Why matter has shape.
Why atoms, molecules, and you exist.
So this little “½ spin” is not a small detail — it’s the reason the universe doesn’t blur into one continuous blob.
Imagine It Like This
Picture a dancer doing a full spin.
After one turn, they face you again — all looks normal.
Now imagine a quantum dancer. After one spin, their state has inverted — like a mirror version of themselves.
Only after the second spin do they return fully to normal.
That’s a half-integer spin particle — it lives in a world where orientation is deeper than direction.
Where identity itself is twisted by geometry.
Why It Matters
Half-integer spin particles — the fermions — form everything we see:
- Electrons → Build atoms.
- Protons & Neutrons → Form atomic nuclei.
- Quarks & Leptons → Make up the universe’s structure.
Without their exclusion principle, chemistry wouldn’t exist, stars couldn’t form, and you wouldn’t be you.
The world of solidity, variety, and individuality — all of it springs from half-integer spin.
The Other Side: Integer Spins
In contrast, particles with integer spins (like photons and gluons) are bosons.
They don’t mind sharing the same state — in fact, they love to.
That’s why light waves can merge, amplify, or laser into coherence.
Bosons unify; fermions separate.
Together, they make the universe dynamic — one family building matter, the other carrying forces.
In Summary
| Property | Half-Integer Spin (½, 3⁄2…) | Integer Spin (0, 1, 2…) |
|---|---|---|
| Particle Type | Fermions | Bosons |
| Example | Electron, Proton, Neutron | Photon, Gluon, Graviton |
| Obeys Pauli Exclusion? | ✅ Yes | ❌ No |
| Builds Matter or Forces? | Builds Matter | Carries Forces |
| Rotation Needed to Return to Original State | 720° | 360° |
Simple Definition
Half-integer spin is a quantum property of particles that makes them behave uniquely — they must spin twice to return to their original state, and they cannot share the same space or state with identical particles.
It’s not about movement — it’s about the identity code of matter.
It defines why every electron in an atom is distinct, why every atom has structure, and why reality is made of individuality rather than sameness.
Final Thought
That subtle half — that ½ twist in the heart of matter — is the universe’s built-in rule of diversity.
It’s the reason form exists, boundaries hold, and individuality has meaning.
In a cosmos that dances between unity and distinction,
half-integer spin is the rhythm that gives matter its soul.